I have the physical Code 55 turnouts myself, and they all seem to be the same frog. It would be strange to engineer products with such tiny differences in frog numbers, it seems to me.
I checked my measurements and found I was wrong on the small one.
Corrected:
small–#5.7
medium–#5.65
large–#6.6
So then I would call them #6S, #6L, #7
Apolgies for the error.
Ed
One could name them Larry, Moe, and Curly – but it wouldn’t change what the manufacturer (and every other modeler) calls them. I don’t see any good reason to add confusion, personally.

Sorry for causing so much consternation.
At least I’ve found something regarding my initial question. It seems somebody has investigated model dimensions vs prototypical dimensions:
As for the other, I’ll go with the dull Peco nomenclature. [:(]
Robert
Robert,
Consternation frequently leads to knowledge, so I will be thanking you.
I do not work in N. I had no idea how “free form” some N scale trackage was. Now I do. My assumption that HO track switches are (close to/trying to be/are) NMRA correct will not be automatic, anymore.
And I especially appreciate your finding the NMRA document. I expect to be hand building some switches in the future, and I’ll take all the help I can get.
Ed
after hand laying turnouts, i looked at Variations in turnout dimensions. The frog number describes the angle at the frog, not a distance.
the following diagram illustrates how NMRA turnout dimensions appear inconsistent depending on frog number. The red closure rail is drawn with the proper prototype radius (see Catskill below) indicating where the frog should be located. Most seem short (see bottom plots).

The Catskill Archive describes how prototype turnout dimensions are calculated (show below).

The radius (leftmost number) between the points and frogs can vary leading to various length (middle number) turnouts that are all the same frog number. Blue section of closure rail is curved and red section is straight.

The key dimensions describe the distance between the points and frog. That distance, the length of the diverging rails and those preceding the points may vary between manufactures and all be the same frog number.
More neat info!
Thanks, Greg
Ed
Doesn’t seem like anyone mentioned, but the angle oof the frog is Arctan(1/frog number). So a #6 angle is arctan(1/6) or 9.46 degrees, and a #4 is arctan(1/4) or 14 degrees. All derived from the definition of the various Trigonometry functions and the basic fact that the frog number indicates how far along (adjacent side) you go to get 1 unit (the opposite side) apart. Since Tangent of the angle is opposite over adjacent (in the case of a #6, 1/6), then the angle by definition is the inverse tangent (arctan) of opposite over adjacent. Those that had Trig may remember SOHCAHTOA - Sine = opposite/hypotenuse, Cosine = adjacent/hypotenuse, and Tangent = opposite/adjacent.
–Randy
–Randy
9.46 degrees is 9 deg 27.6 min.
For a #6 frog:
If the frog angle is based on measuring back to the frog point from the midpoint of the line that forms the “1 unit” location, one gets 9 deg 32 min.* See:
http://www.pcrnmra.org/pcr/clinics/Kolm-TurnoutsWhatYouNeedtoKnow-PCR2008-handout.pdf
If the frog angle is based on measuring back along either rail to the frog point at the “1 unit” location, one gets 9 deg 34 min.
While pokin’ around, I found this neat item on trackwork:
Ed
- Calculations deriving 9 deg 32 min for #6 switch:
tan x = .5/6
x = 4 deg 46 min
frog angle = 2x = 2 (4 deg 46 min) = 9 deg 32 min
From Railway Track and Maintenance by RR Russell Tratman
Frog Number Frog Angle
#5 11 deg 25 min
#6 9 deg 32 min
#8 7 deg 10 min
#10 5 deg 44 min
#20 2 deg 52 min
Chart in book is in 1 deg increments from 5 to 20
Tratman lists three ways of measuring frog number . #1 is “measure the distance, in inches, between between the points where the width over gauge lines is 2 in and 3 in, this distance giving the frog number.”
In drawing posted by 7j43k - where A is 2 inches and B is 3 inches, C is the Frog Number.
after re-reading Ed’s post, I realize this is what he was describing
the discrepancy between what Randy reported, 9.46 deg or 9d 27", and the other value of 9.53 or 9d 32" is that the frog angle is not calculated as a right triangle. There’s no assumption that a frog is on a right or left handed turnout, but the same as if for a wye. Makes less of a difference for smaller angles
frog angle = 2 * atan (0.5 / frog-number)
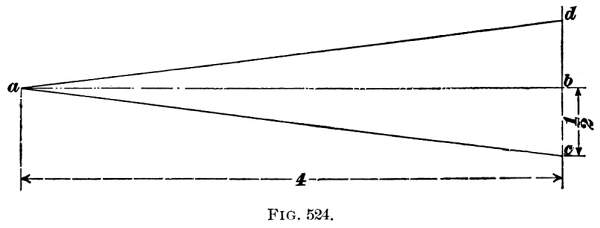
frog angles based on right-angle and isosceles triangles
4 14.04 d 14d 2" 14.25 d 14d 15"
5 11.31 d 11d 19" 11.42 d 11d 25"
6 9.46 d 9d 28" 9.53 d 9d 32"
7 8.13 d 8d 8" 8.17 d 8d 10"
8 7.13 d 7d 8" 7.15 d 7d 9"
9 6.34 d 6d 20" 6.36 d 6d 22"
10 5.71 d 5d 43" 5.72 d 5d 43"
20 2.86 d 2d 52" 2.86 d 2d 52"
I just use the printable turnout plans from fast tracks, cut ties to match, build the frog with the frog jig, points with point jig and eyeball the rest.
To distill the original question to its essential essence:
I handlay all of my specialwork, so I’m certain that my #4 turnouts (on my end-of-the-coal-hauler module, built in 1980) and my #5 turnouts (in the hidden staging yards at Nonomura, built within the last decade) are built to the proper dimensions.
That said, one of my long-wheelbase 2-Co+Co-2 EF18 or EF58 class juice jacks can slither through a #5. Trying to force it through the curved route of a #4 will put it on the ground, every time.
Why? Those motors require an honest 24 inch (610mm) radius to operate. The closure rail of a #4 turnout has a radius too tight for the long rigid wheelbase. The axle under the center of the carbody gets pinched over the rails on whichever truck hits the tight spot first.
Chuck (Modeling Central Japan in September, 1964)